Firmas digitales: La explicación definitiva

¿Qué es una firma digital?

Las firmas digitales son una de las piedras angulares de nuestra civilización tecnológica. En este artículo vamos a analizar su funcionamiento, que es más fácil de lo que puede parecer.

Las construcciones de firma digital usan dos tipos de claves:

• Clave Privada (prv): Se usa para firmar mensajes, y debe mantenerse en secreto para que nadie pueda firmar haciéndose pasar por nuestra identidad.
• Clave Pública (pub): Sirve como una identidad digital que puede compartirse por Internet.

Estas dos claves están vinculadas matemáticamente, pero pub no revela información sobre prv.

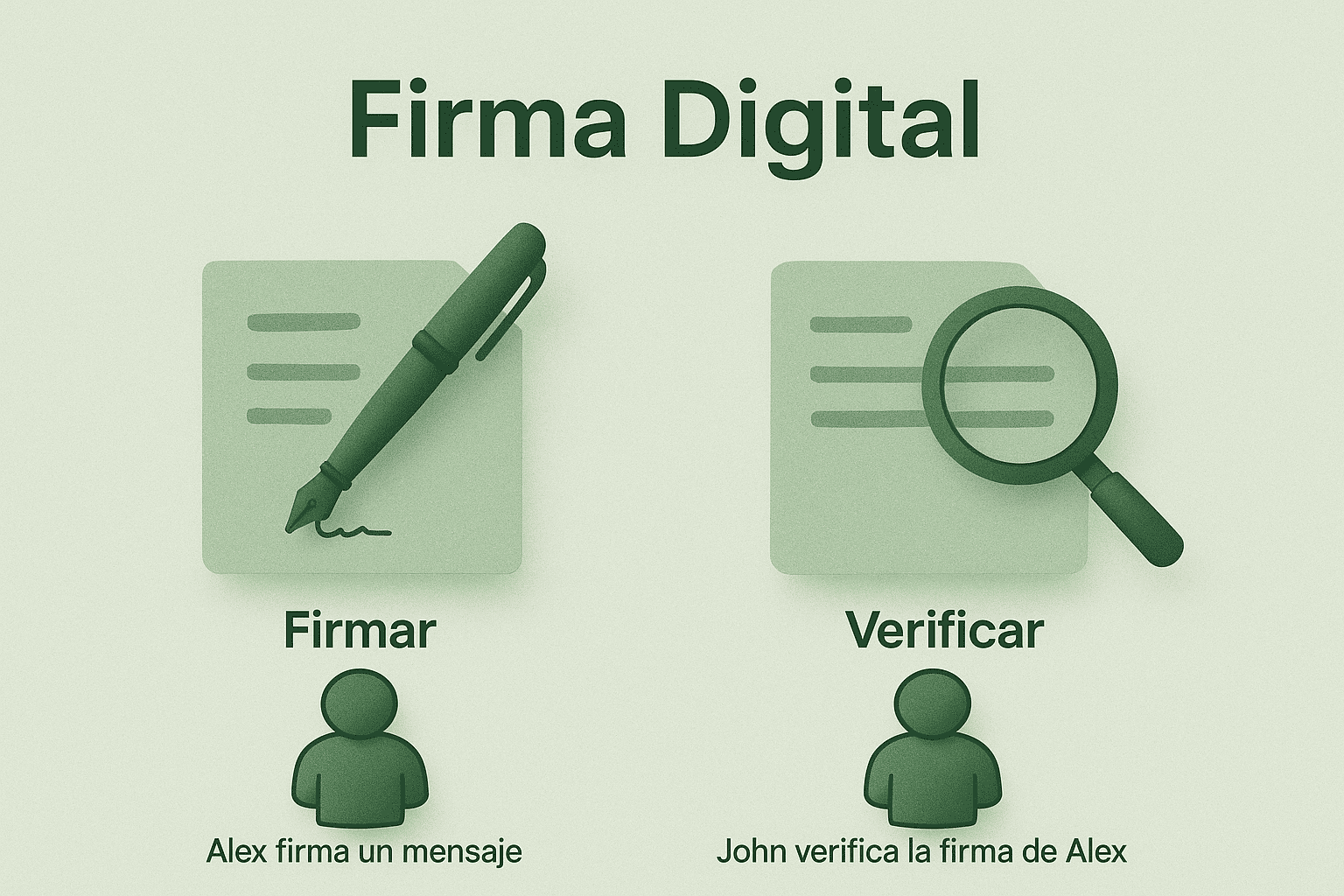
Estas claves son simplemente números (muy grandes), al igual que el identificador del mensaje firmado msg y la firma sig. Con estos datos podemos crear firmas o verificarlas:

• Firmar: msg + prv = sig
• Verificar: msg + pub + sig = True / False

Si la verificación da True como resultado, no hay dudas de que el firmante pub ha firmado el mensaje msg usando su clave privada prv (sea cual sea).

Una firma digital tiene las siguientes propiedades:

• No repudio: La firma digital es una prueba matemática irrefutable de que pub ha firmado un mensaje msg.
• Integridad: El mensaje firmado no puede alterarse. O mejor dicho, la firma sólo es válida para el msg escogido por el firmante.
• Autenticidad: La identidad firmante no puede alterarse. La firma sólo es válida para ese pub.

Debido a estas cualidades, las firmas digitales se usan para acreditar la identidad de webs HTTPS por medio de certificados digitales, para autorizar transacciones en tu banco o en una blockchain, para autenticarse al acceder a servidores en la nube, para verificar que una actualización de software proviene de los desarrolladores autorizados, etc.

Sin firmas digitales, Internet sería un lugar mucho más intervenido por los Estados, que proveerían métodos de autenticación basados en su control de la población, en vez de en las matemáticas. Se limitaría el acceso al Internet seguro y no existirían las criptomonedas.

---

Este artículo se enfoca en un tipo específico de firma digital: las que utilizan la Criptografía de Curva Elíptica – ECC por sus siglas en inglés. Este tipo de firmas son las más eficientes con respecto a la seguridad que ofrecen, y por ello se usan en todas las blockchains y en gran parte de Internet.

¿En qué se basa la Criptografía de Curva Elíptica?

Aunque suene complicado, el funcionamiento de las firmas digitales es fácil de entender una vez conocemos la base de la ECC.

¿WTF es una curva elíptica?

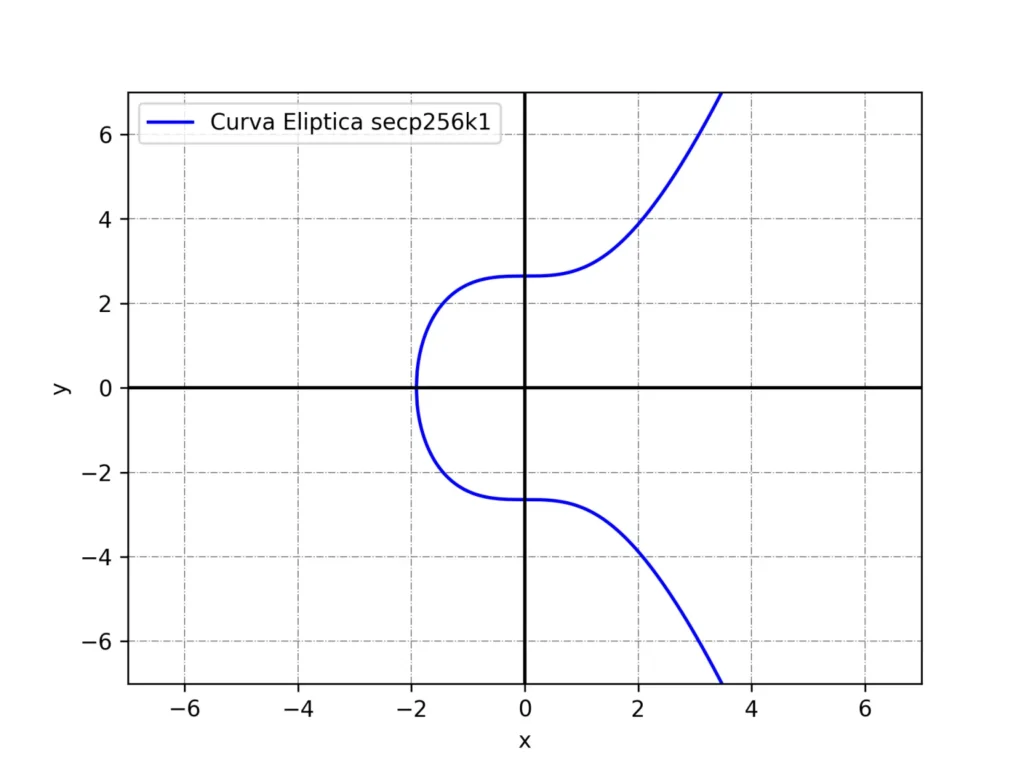
Una curva elíptica 🍌 es simplemente una función del tipo:

$y^2 = x^3 + ax + b$, donde $a$ y $b$ son constantes.

Por ejemplo, la curva elíptica usada en Bitcoin y Ethereum, con $a = 0$ y $b = 7$, se ve de la siguiente forma en el plano.

Este tipo de curvas fueron estudiadas en los siglos 19 y 20 por verdaderos esquizofrénicos, y después, en los años 80 se descubrió que las propiedades de las curvas elípticas se podían usar para crear construcciones criptográficas.

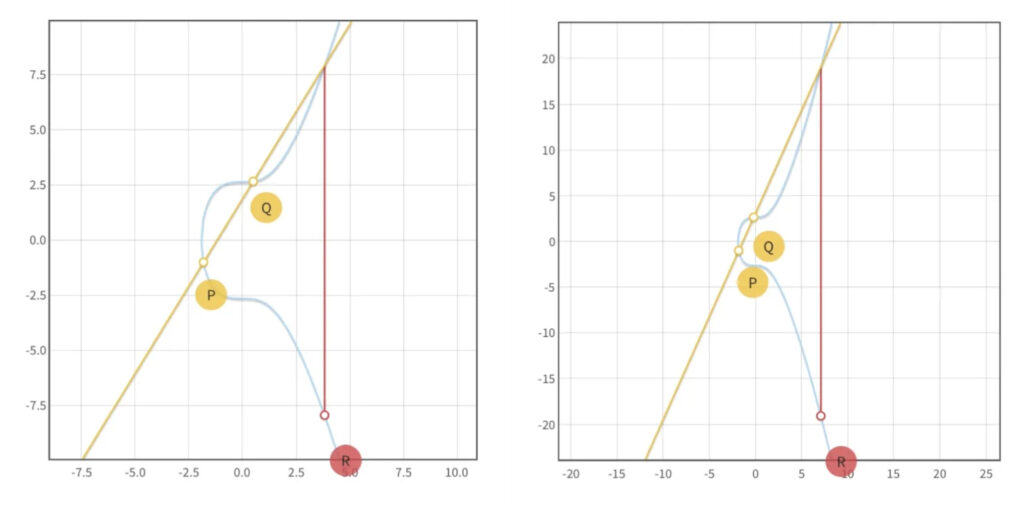
Más en concreto, lo que nos concierne es una operación que se realiza con estas curvas y que se conoce como suma de puntos. Esta operación toma dos puntos de la curva, $P = (x_P, y_P)$ y $Q = (x_Q, y_Q)$, y obtiene un tercer punto de la curva $R = (x_R, y_R)$.

La fórmula para calcular la suma de puntos (las coordenadas del nuevo punto $R$), que NO es necesario saber, es:

$x_R = λ^2 – x_P – x_Q$

$y_R = λ(x_P – x_R) – y_P$

Donde

$λ = \frac{y_Q – y_P}{x_Q – x_P}$ si $P ≠ Q$

$λ = \frac{3x_P^2 + a}{2y_P}$ si $P = Q$

($a$ es la constante de la curva elíptica).

Curvas en Campos Finitos

Las curvas elípticas que vemos en las imágenes están definidas sobre el campo de los números reales. En otras palabras, las coordenadas $x$ e $y$ son números reales, los cuales pueden tomar valores infinitamente grandes y tener precisión decimal infinita. El problema es que un ordenador no puede usar dígitos ilimitados.

Para que el ordenador pueda hacer cálculos con puntos del plano, la cantidad de dígitos de las coordenadas debe ser limitada y manejable.

Por este motivo usamos los Campos Finitos, que consisten en una serie finita de números enteros – números no negativos y sin decimales. Por ejemplo, un Campo Finito puede estar compuesto de los números $\{0, 1, 2, 3, 4, 5, 6\}$.

El número de elementos en el Campo Finito se conoce como el orden del Campo Finito, y se denota con $p$. En este ejemplo el orden del Campo Finito es $p = 7$, y el rango de los números es $[0, 7)$.

Para representar curvas elípticas en un eje de coordenadas, los valores de $x$ e $y$ estarán en un Campo Finito. Este eje tendrá un número finito de puntos que representar (en nuestro ejemplo habría 7×7 puntos posibles).

Ahora, en el Campo Finito, la curva elíptica se verá como una serie de puntos desperdigados cuyas coordenadas cumplen la ecuación de la curva ($y^2 = x^3 + ax + b$), como veremos más adelante.

¿Cómo se opera en los Campos Finitos?

En el ejemplo del Campo Finito de orden $7$, que consiste en los números $\{0, 1, …, 6\}$, fijémonos que al sumar 5 + 2 nos salimos del rango! Para mantenernos en el rango siempre, en los cálculos del Campo Finito usamos aritmética modular, también llamada aritmética de reloj.

De la misma forma que cuando llegamos a las 12 horas en un reloj analógico volvemos al 0, nuestras operaciones en el Campo Finito también harán esto cuando se llegue al número $p$. En nuestro ejemplo, como $p = 7$, el resultado de 5 + 2 es 0.

Al operar sobre números dentro del rango obtendremos resultados fuera del rango, y matemáticamente el resultado se devuelve al rango con un operación llamada reducción modular – representada con $mod$.

La reducción se puede calcular restando o sumando al número fuera de rango $p$ repetidamente hasta que entre en el rango. Por ejemplo:

• Restando: $17 \mod 7 = 10 \mod 7 = 3$
• Sumando: $-6 \mod 7 = 1$

Esto es lo mismo que dividir el número entre $p$ y tomar el resto: $17 \div 7$ da un resto de $3$. $-6 \div 7$ da un resto de $1$ (y un cociente de $-1$).

Por lo tanto, sumas, restas y multiplicaciones modulares son iguales a las que conocemos pero con una reducción. Un caso algo especial es la división modular, que se explica abajo.

Explicación de la División Modular

La división es la operación inversa a la multiplicación. Por ello la división puede expresarse como una multiplicación por la inversa: a / b = a * b-1, donde b-1 es la inversa multiplicativa de b.

La inversa multiplicativa es el número que cumple que b * b-1 = 1. Todos los números reales, salvo el 0, tienen una inversa. El 0 no tiene inversa porque no existe un número que multiplicado por 0 de 1. En concreto, cualquier número real k ≠ 0 tiene como inversa el número 1 / k. Como la división en realidad es una multiplicación por la inversa, esto implica que podemos dividir por cualquier número salvo el 0.

En un Campo Finito, la inversa se conoce como inversa modular y cumple que b * b-1 = 1 mod p. Para dividir en el Campo Finito calculamos la inversa modular, que se obtiene con un par de algoritmos, y multiplicamos por ella. Por lo tanto a / b mod p se define como a * b-1 mod p.

Sin embargo, en el Campo Finito solo existen inversas modulares para todos los números (menos el 0) cuando su orden p es primo. Lo que significa que sólo podemos dividir cuando p es un número primo. Eso es todo.

Representación

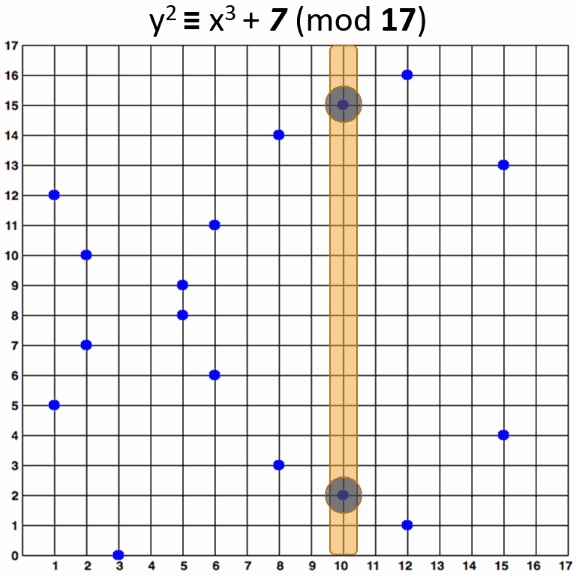
En la siguiente imagen podemos ver la representación de la curva $y^2 = x^3 + 7$ definida sobre el Campo Finito de orden 17. Por ejemplo, el $(3, 0)$ es un punto de la curva porque $3^3 + 7 = 0 \mod 17$.

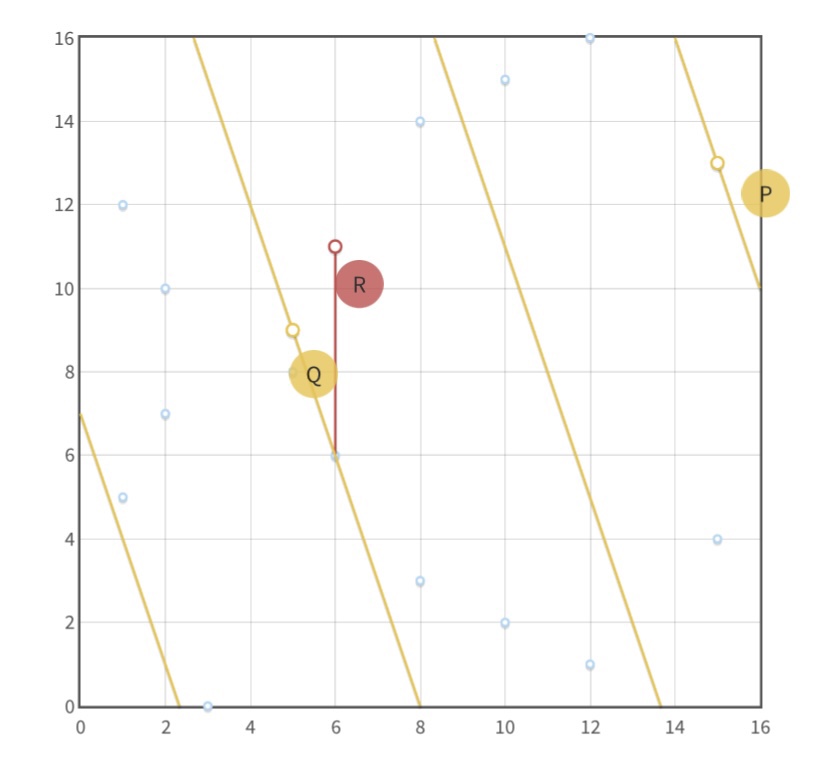
Fijémonos que los puntos exhiben simetría respecto al eje $x$. Esto se debe a que en la fórmula tenemos $y^2$. Si en los números reales $y^2 = (-y)^2$, en el Campo Finito $y^2 = (p – y)^2$.

Por ejemplo:

• $3^2 \mod 5 = 4$
• $(5 – 3)^2 \mod 5 = 4$

Por lo tanto, si tenemos un punto de la curva $(x, y)$, también tendremos un punto $(x, p -y)$. Esto provoca que los puntos se vean reflejados como en un espejo. La única excepción es cuando $y = 0$, ya que $p – 0 \mod p = 0$ (por lo tanto no es una coordenada $y$ distinta).

---

Con esto ya tenemos todo lo que necesitamos, así que tómense un Blue Label porque el resto es muy chill. A modo de resumen tenemos:

1. La fórmula para calcular la suma de puntos de la curva elíptica
2. El Campo Finito donde se realizan estos cálculos modulo $p$ (un número primo)

Una fucking función unidireccional

Lo que los criptógrafos construyeron con estas piezas es una función unidireccional, es decir, una función que sólo se puede calcular en un sentido, conocida como multiplicación de curva elíptica.

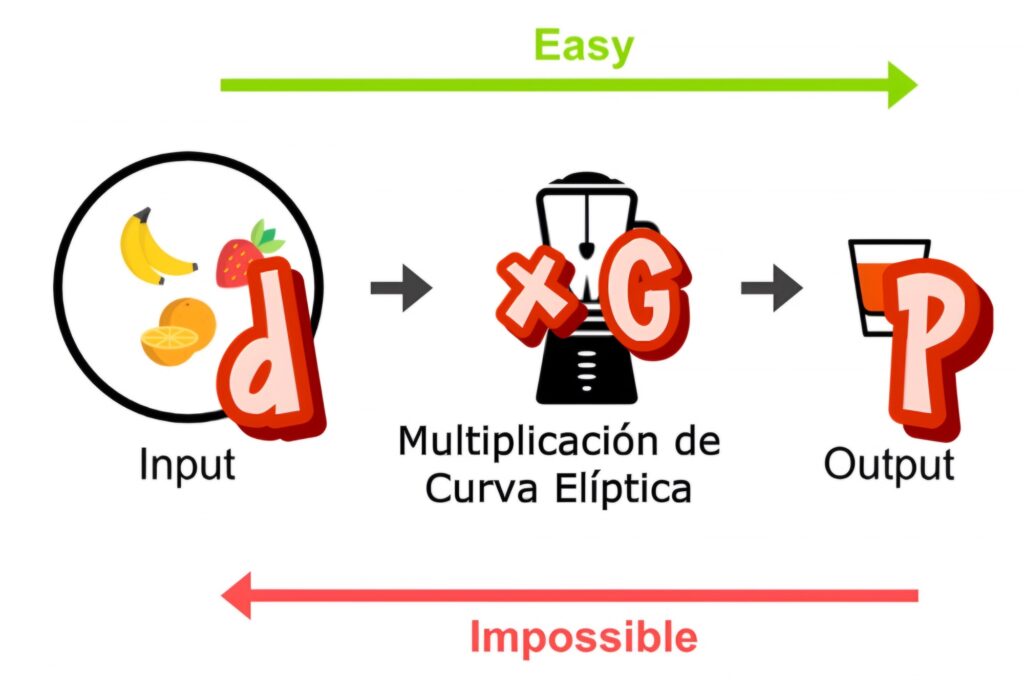
En concreto, si tenemos un número $d$ y un punto de la curva elíptica $G$ que es una constante pública, la función unidireccional consiste en sumar $G$ consigo mismo $d – 1$ veces (usando las formulas de la suma de puntos).

Esta operación se denota como $d \times G$ y da como resultado otro punto $P$ de la curva elíptica.

El punto $G$ (😳), que es distinto para cada curva elíptica, recibe el nombre de punto generador ya que todos los puntos que usaremos serán «múltiplos» de él.

Spoiler: el número $d$ es una clave privada y el punto de la curva elíptica $P = d \times G$ es la clave pública.

El Camino Fácil

Imaginemos que $d = 9$. Como empezamos con el punto $G$, podemos calcular $P = 9 \times G$ sumando $G$ 8 veces. Pero es más rápido hacer lo siguiente:

1. Empezamos sumando $2G = G + G$
2. Ahora sumamos el punto $2G$ consigo mismo, obteniendo $4G = 2G + 2G$
3. De nuevo sumamos el punto $4G$ consigo mismo, obteniendo $8G = 4G + 4G$
4. Finalmente calculamos $9G = 8G + G$

Y ya estaría! Los algoritmos que usan este atajo requieren de menos y menos sumas adicionales a medida que el valor de $d$ crece. Si $d$ fuera un número muy grande, sería imposible calcular $P$ por medio de las sumas repetidas, pero estos algoritmos que usan atajos lo calcularían en una fracción de segundo (en un ordenador, claro).

Es gracias a que conocemos $d$ que podemos calcular el atajo a tomar y llegar a $P = d \times G$ de forma rápida.

El Camino Difícil

Si lo que conocemos es $P$, y no conocemos $d$, entonces el punto $P$ no revela información sobre cuantas veces se ha necesitado sumar $G$ consigo mismo.

La única forma aparente de descubrir ese número de veces es probar a sumar $G$ muchas veces y comprobar si algún múltiplo de $G$ es igual a $P$ (en cuyo caso ya sabremos cuantas veces se ha necesitado sumar $G$). Esto se conoce como ataque de fuerza bruta porque tenemos que calcular $d \times G$ por cada posible valor de $d$.

Pero en la práctica el orden del Campo Finito no es de 7 ni de 17, sino de un número de 77 dígitos. Y una curva elíptica en un Campo Finito tan grande estará conformada por muchos puntos — que satisfacen su ecuación.

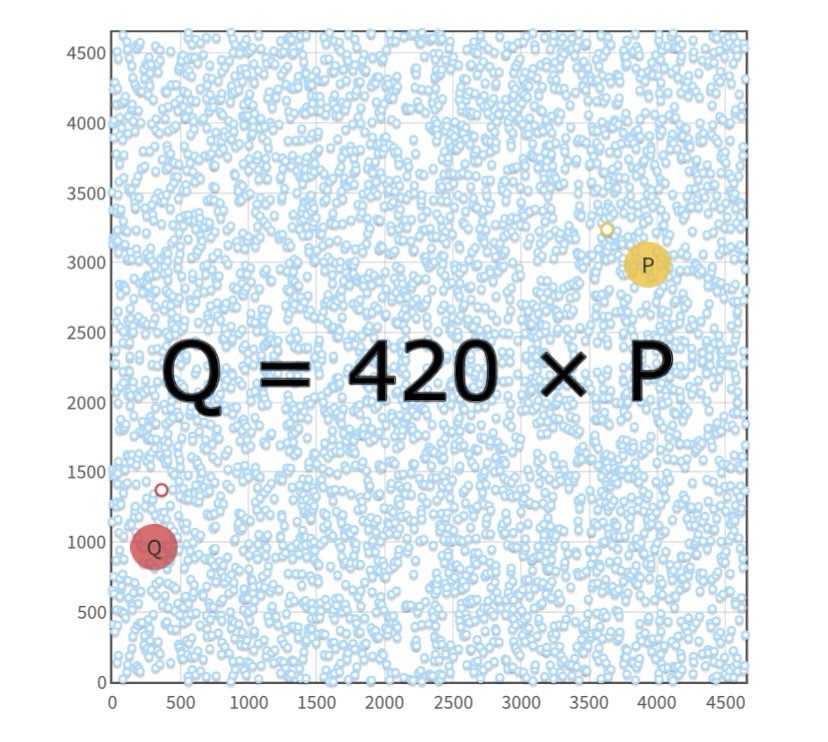
Por ejemplo, en el caso de Bitcoin y Ethereum, la cantidad de puntos en la curva Secp256k1 equivale al número primo $n$ = 115792089237316195423570985008687907852837564279074904382605163141518161494337.

Sí, ese es el número de puntos en Secp256k1. En esta curva, cada uno de estos $n$ puntos es un múltiplo de $G$ único. Por lo tanto, existen $n$ posibles valores de $d$ (que dan como resultado $n$ posibles puntos $P = d \times G$).

Para ponerlo en perspectiva, hay más posibles valores de $d$ que átomos en el universo entero.

Al ser $d$ un número dentro de un rango tan gigantesco, la cantidad de múltiplos de $G$ que tendríamos que calcular para ejecutar un ataque de fuerza bruta es inconcebible. Calcular una parte significativa de los $n$ posibles múltiplos es imposible de realizar sin tardar millones de años, incluso si usásemos los superordenadores más potentes que existen.

De la función unidireccional a las firmas digitales

Ahora sí que sí, ha llegado el momento que todos estábamos esperando 😎🤝😎. Presten atención porque ahora se desvela la clave de todo.

Como ya hemos adelantado antes, el número $d$ es la clave privada mientras que el punto $P = d \times G$ es la clave pública. Gracias a nuestra función unidireccional es imposible calcular la clave privada de nadie a partir de su clave pública.

• Clave Privada = $d$
• Clave Pública = $P$ (resultado de $d \times G$)

El truquito

Para empezar a construir un esquema de firma digital veamos este ejemplo:

1. Alex: Elige una clave privada $d$ al azar en el vasto espacio de posibles valores. Calcula el punto $P = d \times G$ realizando varias sumas del punto generador $G$. Entonces comparte ese punto $P$ (su clave pública). También comparte un número $e$, que representa un mensaje.
2. Juan: Recibe el punto $P$ y el número $e$ de Alex. Con estos datos calcula un nuevo punto $e \times P$.

El nuevo punto calculado por Juan es también un múltiplo de $G$:

$e \times P$ $=$

$e \times (d \times G) =$

$(e \cdot d) \times G$

Juan, sin conocer el múltiplo $d$ de $G$, lo está incrementando por $e$ (al sumar $P$ consigo mismo el equivalente a $e – 1$ veces). Juan tampoco sabrá cuál es el nuevo múltiplo porque depende de $d$.

Llamemos al nuevo múltiplo de $G$, $s = (e \cdot d)$.

1. Alex: Comparte $s$, que sólo él puede calcular usando su clave privada $d$.
2. Juan: Verifica que $e \times P$ $=$ $s \times G$ (deben ser el mismo punto).

La idea general es que si alguien nos muestra un valor $s$, que cumpla que el punto $s \times G$ es el mismo que $e \times P$, eso significa que $s$ es el mismo múltiplo de $G$ que subyace a $e \times P$. Por lo tanto, la persona que ha publicado $s$ ha necesitado conocer el valor $d$ asociado a $P$.

Así Juan comprueba que Alex conoce $d$ – ya que es necesario para calcular $s$. Si por el contrario Alex usa un valor $s_{fake} = (e \cdot d_{fake})$ que no es el correspondiente a $P$, entonces:

$e \times P$ $≠$ $s_{fake} \times G$

Simplemente porque:

$(e \cdot d) \times G$ $≠$ $(e \cdot d_{fake}) \times G$

El nonce

Hay un problema en el esquema anterior: una vez $s$ es público, cualquiera puede calcular la clave privada como $d = \frac{s}{e}$ (que se deriva de $s = e \cdot d$).

Para ocultar el valor de la clave privada usamos el nonce, un valor secreto que se usa una sola vez. El nonce se denota como $r$ y está contenido en el mismo rango que $d$.

Añadimos el nonce en el cálculo de $s$ para que haya otra incógnita:

$s = (e \cdot d)$ $+$ $r$

Ahora $d = \frac{s – r}{e}$ y como $r$ es secreto, no se puede calcular $d$. De nuevo, olvidémonos de probar muchos posibles valores del nonce ya que esto sería un ataque de fuerza bruta (por cada clave privada calculada tenemos que comprobar si el múltiplo de $G$ coincide con $P$).

Fijemonos que ahora:

$s \times G$ $=$

$(e \cdot d) \times G$ $+$ $r \times G$

Atentos al procedimiento final:

1. Alex: Elige al azar $d$ y $r$. Calcula $P = d \times G$ y $R = r \times G$. Publica $P$, $e$, $s$ y $R$.
2. Juan: Verifica que $e \times P$ $+$ $R$ $=$ $s \times G$

Como acabamos de ver, estos dos puntos deben ser el mismo porque:

$s \times G$ $=$

$(e \cdot d) \times G$ $+$ $r \times G$ $=$

$e \times P$ $+$ $R$

De nuevo, la idea es que podemos verificar que el punto $e \times P$ $+$ $R$ es el mismo punto que $s \times G$. La persona que produjo $s$ debía conocer los valores $d$ y $r$ asociados a $P$ y $R$. Gracias a tener una segunda incógnita (el nonce) no se puede despejar $d$ de la fórmula $s = (e \cdot d) + r$.

Ahora sí que hemos construido un esquema de firma digital, ya que estamos demostrando que conocemos la clave privada sin revelarla.

En esta construcción la firma consiste en el par de valores $(s, R)$. Además podemos ver que se cumplen las propiedades que vimos al principio:

• No repudio: No hay duda de que alguien que conoce la clave privada $d$ asociada a $P$ ha firmado el mensaje, porque $s$ no puede calcularse sin conocer $d$.
• Integridad: La firma sólo es válida para el mensaje $e$ escogido por el firmante a la hora de calcular $s$, ya que $(e \cdot d) \times G$ $≠$ $e_{fake} \times P$.
• Autenticidad: La firma sólo es válida para la clave pública $P$, ya que $(e \cdot d) \times G$ $≠$ $e \times P_{fake}$.

Operaciones modulo $n$

Para ser más precisos recordemos que hay $n$ posibles múltiplos de $G$, que van desde $0 \times G$ hasta $(n – 1) \times G$. El grupo de múltiplos de $G$ es cíclico, lo que significa que:

• $n \times G =$ $0 \times G$
• $(n + 1) \times G =$ $1 \times G$
• $(n + 2) \times G =$ $2 \times G$
• etc.

Por ello:

$s \times G = (s \mod n) \times G$

El valor no reducido de $s$ es innecesariamente grande, ya que su valor reducido modulo $n$ es equivalente. Por esto, en la práctica $s$ se calcula con:

$s = (e \cdot d) + r \mod n$

El esquema Schnorr

El esquema que hemos construido se conoce como Schnorr, y se usa en Bitcoin y otras blockchains debido a su eficiencia y simplicidad.

El procedimiento exacto de Schnorr es el siguiente:

1. El firmante tiene una clave privada $d$ y su correspondiente clave pública $P = d \times G$
2. El firmante genera un número secreto $r$ llamado nonce (number used once) y calcula $R = r \times G$
3. Ahora escoge un mensaje, añade $R$ al mensaje, y calcula su huella digital $e$ (también conocido como hash del mensaje)
4. Finalmente calcula $s = (e \cdot d) + r \mod n$
5. La firma digital consiste en los valores $s$ y $R$

Ahora, la forma de verificar que esta firma es correcta es simplemente comprobando que:

$s \times G = e \times P + R$

Tamaño de las Claves y Firmas

La clave privada es un número de 256 bits, o 32 bytes. La clave pública es un punto, compuesto de dos coordenadas de 32 bytes cada una (por lo tanto, 64 bytes). Técnicamente los puntos se pueden comprimir y representar con tan sólo 33 bytes.

Por otro lado la firma consiste en un número y en otro punto. Esto son 96 bytes si el punto no se comprime o 65 bytes si se comprime.

La compresión se debe a que cualquier punto $(x, y)$ de la curva tiene un punto “reflejo” $(x, p – y)$. Por lo tanto una coordenada $x$ válida tiene dos puntos asociados, que sólo difieren en su coordenada $y$.

A nivel práctico esto significa que podemos usar sólo la coordenada $x$, y un bit para representar uno de los dos hemisferios posibles de la coordenada $y$.

Otros esquemas

Una variación de Schnorr es el esquema EdDSA, que usa unas curvas elípticas especiales (Ed25519, Ed448) para conseguir una mayor eficiencia. También se considera más resiliente frente a los side channel attacks, ataques en los que se extrae información sobre la clave privada observando cuánto tiempo tarda un dispositivo en firmar, cuanta energía consume, emisiones electromagnéticas, etc.

Pero el esquema que se lleva el puesto de más usado es ECDSA – Elliptic Curve Digital Signature Algorithm. El motivo de existir de ECDSA, de acuerdo con Andrew Poelstra, es que el creador de las firmas Schnorr, que llevan su nombre, las patentó. Y como nadie quería tocar criptografía patentada se creó ECDSA, que era mucho más complicado que Schnorr para evitar parecerse y violar la patente.

Pero al complicar las cosas, ECDSA perdió características importantes que Schnorr tiene, como la capacidad de agregar firmas digitales de varios participantes en una firma conjunta (cosa que es muy valiosa en la blockchain).

Las patentes de Schnorr ya han expirado y por ello Schnorr se está usando en Bitcoin y otras blockchains. Pero por motivos históricos y de estandarización lo más usado en Internet es ECDSA 🤮.